python的一个简单的线性回归示例

内容：用最小二乘法求解出关于样本数据回归方程的参数
工具：pycharm
库：numpy，matplotlib.pyplot，statsmodels.api
一：导入库
import numpy as np # NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。
import matplotlib.pyplot as plt # Matplotlib 是 Python 的绘图库。 它可与 NumPy 一起使用，提供了一种有效的 MatLab 开源替代方案。 它也可以和图形工具包一起使用，如 PyQt 和 wxPython。
import statsmodels.api as sm


二：准备样本数据


# 30个样本点
nsample = 30
# linspace 用于创建一个一维数组，数组是一个等差数列构成的
x = np.linspace(0, 10, nsample)
#给列表x添加一列1
X = sm.add_constant(x)
#创建一个array
beta = np.array([2, 5])
#误差项e,生成nsample个数值，数值符合正态分布
e = np.random.normal(size = nsample)
 # 生成实际样本值y, X与beta点乘 ，再加上一个误差项,
y = np.dot(X, beta) + e

x：样本参数，y：样本值，一一对应，构成样本集

样本打印：

x
array([ 0.        ,  0.34482759,  0.68965517,  1.03448276,  1.37931034,
        1.72413793,  2.06896552,  2.4137931 ,  2.75862069,  3.10344828,
        3.44827586,  3.79310345,  4.13793103,  4.48275862,  4.82758621,
        5.17241379,  5.51724138,  5.86206897,  6.20689655,  6.55172414,

y

array([ 1.73861916,  3.98933469,  4.01607466,  7.38780274,  7.85185995,
       11.84179195, 12.8360651 , 12.91377603, 15.76041099, 17.49382018,
       18.28809969, 21.65472398, 23.47266075, 25.56485442, 24.29500412,
       29.71403133, 31.17525199, 29.71997152, 34.17033771, 33.59499877,
       36.55552835, 37.5732812 , 39.76235192, 41.96783255, 44.14114623,
       45.42177332, 44.80687386, 47.13221782, 50.75426909, 52.18024037])





三：拟合数据

# 用最小二乘法定义出 model
model = sm.OLS(y, X)
# 拟合 res = model.fit()
#拟合估计值y_
y_ = res.fittedvalues

拟合后得到的回归方程参数值打印

pams
array([1.88609347, 5.04209344])
拟合后的估计值打印

y_

array([ 1.96863567,  3.68982173,  5.41100779,  7.13219384,  8.8533799 ,
       10.57456595, 12.29575201, 14.01693806, 15.73812412, 17.45931017,
       19.18049623, 20.90168229, 22.62286834, 24.3440544 , 26.06524045,
       27.78642651, 29.50761256, 31.22879862, 32.94998467, 34.67117073,



四：绘制线性回归图


#画图
fig, ax = plt.subplots(figsize = (8, 6))
 #原始数据x 与 y
ax.plot(x, y, 'o', label = 'data')
#拟合数据
ax.plot(x, y_, 'r--.', label = 'test')
ax.legend(loc='best')
plt.show()

描述：线性回归图

图片：1.png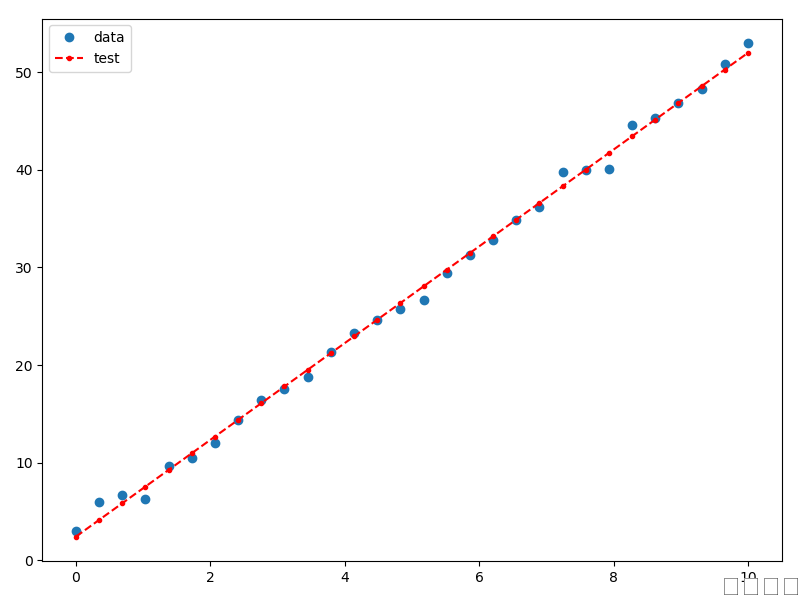

ps: 昨天账号密码忘了，今天重置了才能发帖，多多包涵!